Solving Systems of Linear Inequalities
Example 1
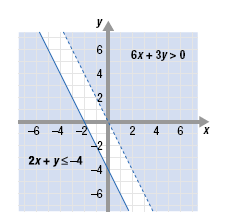
Graph the system of inequalities.
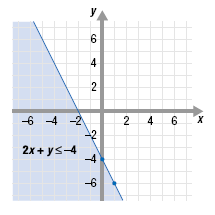
2x + y ≤ -4
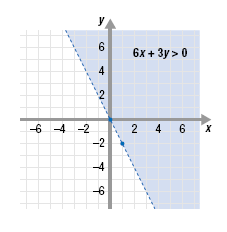
6x + 3y > 0
Solution
Step 1 Solve the first inequality for y. Then graph the inequality.
To solve 2x + y ≤ -4 for y, subtract 2x from both sides.
The result is y ≤ - 2x - 4.
To graph y ≤ - 2x - 4, first graph the equation y
= - 2x - 4.
• Plot the y-intercept (0, -4). Then use the slope,
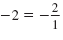 to plot a
second point at (1, -6). to plot a
second point at (1, -6).
For the inequality y ≤ - 2x - 4, the inequality symbol is “≤â€.
This stands for “is less than or equal to.â€
• To represent “equal to,†draw a solid line through (0, - 4) and
(1, - 6).
• To represent “less than,†shade the region below the line.
Step 2 Solve the second inequality for y. Then graph the inequality.
To solve 6x + 3y > 0 for y, do the following:
Subtract 6x from both sides. 3y > - 6x + 0
Divide both sides by 3. y > - 2x + 0
To graph y > - 2x + 0, first graph the equation y = 2x + 0.
• Plot the y-intercept (0, 0). Then use the slope,
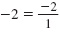 , to plot a
second point at (1, -2). , to plot a
second point at (1, -2).
For the inequality y > - 2x, the inequality symbol is “>â€.
This stands for “is greater than.â€
• Since the inequality symbol “>†does not contain “equal to,â€
draw a dotted line through (0, 0) and (1, -2).
• To represent “greater than,†shade the region above the line.
Step 3 Shade the region where the two graphs overlap.
The shaded regions do not overlap.
So the system of inequalities has no solution.
Example 2
Graph the system of inequalities.
y ≤ x + 5
y < x - 3
Solution
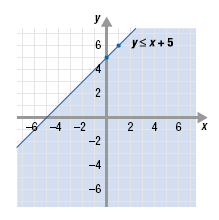
Step 1 Solve the first inequality for y. Then graph.
The graph of y ≤ x + 5 is shown.
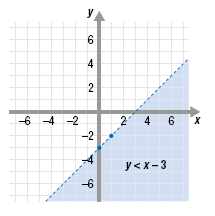
Step 2 Solve the second inequality for y. Then graph.
The graph of y < x - 3 is shown.
Step 3 Shade the region where the two graphs overlap.
The solution is the region below the line y = x - 3 since it is where the
graphs overlap.
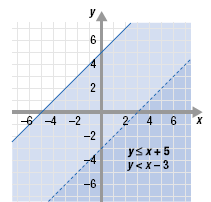
The solution of the systems is the dark region where the graph overlaps.
Example 3
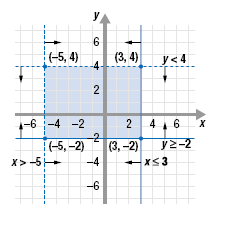
Given the following system of linear inequalities:
x > - 5
x ≤ 3
y < 4
y ≥ 2
a. Graph the system.
b. Find the coordinates of three points that satisfy all four inequalities.
c. Find the points of intersection of each pair of corresponding lines.
d. Find the area of the region whose points are the solution of the system.
Solution
a. Graph each inequality and shade the region where the graphs overlap.
b. Each point in the shaded region is a solution of the system.
For example, (0, 0), ( -2, 1), and ( -4, 1) each satisfy the system.
c. The points of intersection are the corners of a rectangle.
The points are (3, 4), ( -5, 4), ( -5, -2), and (3, -2).
(Note: Only one corner (3, 2), is also a solution of the system.)
d. To find the area of a rectangle, multiply its length by its width.
The length of the rectangle is 8 units; the width is 6 units.
The area is length
width · 8 units
· 6 units = 48 square units.
 |