Dividing Rational Expressions
You probably know how to divide rational expressions containing monomials.
Now, we will use the same procedure to divide rational expressions that
contain binomials or trinomials.
Note:
Here is an example of dividing rational
expressions that contain monomials:
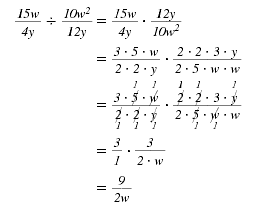
Procedure —
To Divide Rational Expressions
Step 1 Invert the second fraction and change the division symbol,
÷, to the multiplication symbol,
·.
Step 2 Factor the numerators and denominators.
Step 3 Cancel all pairs of factors common to the numerators and
denominators.
Step 4 Multiply the numerators. Multiply the denominators.
We usually leave the answer in factored form.
Example 1
Find:
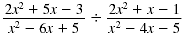
| Solution |
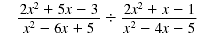 |
| Step 1 Invert the second fraction
and change the division
symbol, ÷, to the
multiplication symbol, · . |
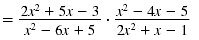 |
| Step 2 Factor the numerators
and denominators.
|
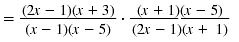 |
| Step 3 Cancel all pairs of factors
common to the numerators
and denominators.
|
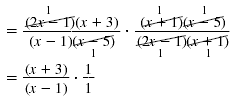 |
| Step 4 Multiply the numerators.
Multiply the denominators. |
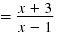 |
Thus,
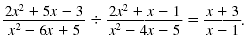
Example 2
Find:
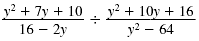
| Solution |
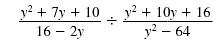 |
| Step 1 Invert the second fraction
and change the division
symbol, ÷, to the
multiplication symbol, ·. |
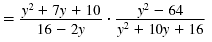 |
| Step 2 Factor the numerators and
denominators.
|
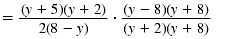 |
| Step 3 Cancel all pairs of factors
common to the numerators and denominators. |
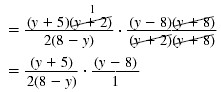 |
Replace
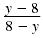 with
-1. with
-1. |
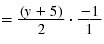 |
| Step 4 Multiply the numerators.
Multiply the denominators. |
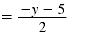 |
Thus,
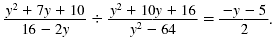
Note:
You can also write the answer as follows:
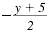 |