Graphing Systems of Equations
Objective Understand the geometric
interpretation of systems of two linear equations in two
variables, and in solving them graphically.
This chapter provides a great opportunity for you to discover
ideas about systems of equations. Make sure that you graph
several systems by yourself, at least one of which has no
solution, and at least one of which has infinitely many
solutions.
Systems of Linear Equations
Key Idea
A pair of linear equations like A + O = 5 and 2A + 3O = 12 is
called a system of linear equations. Its
solution set is the set of all values of the two variables that
satisfy both equations.
So, let us solve the following system of linear equations:
A + O = 5 and 2A + 3O = 12
That is to say, A and O must satisfy the equations
simultaneously. A good way to understand the solution to a system
of equations is to graph both equations on the same axes, as
shown at the right.
What information can be found from this graph?
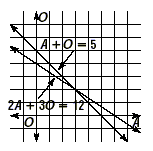
First, the set of points on the graph of A + O = 5 is the set
of all points that satisfy that equation, or the set of all
ordered pairs (A , O ) for which the equation holds true. In the
same way, the graph of 2A + 3O = 12 is the set of all points for
which that equation holds true. Therefore, the solution to the
system of equations is the set of all ordered pairs (A , O ) for
which both equations hold true. The solution to the system must
correspond to a point that lies on both graphs, or that lies on
the intersection of the graphs.
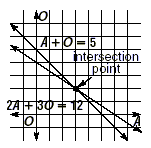
There is only one intersection point, a point that lies on
both graphs. It is the point with coordinates (3, 2), or A = 3
and O = 2.
You should graph these lines and find the coordinates of the
intersection point yourself.
Exercise
Solve graphically the system x + 2y = 1 and 2x + y = 5.
In this case also, there is only one solution.
Is there always only one solution to a system of linear
equations?
Think about the problem graphically. A system of linear
equations corresponds to a pair of straight lines. When there are
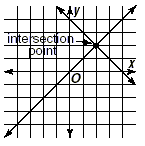
two straight lines, there are three possibilities.
| (1) The lines intersect in exactly one
point. |
(2) The lines are parallel, and do not
intersect at all. |
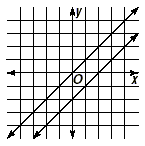
(3) The lines are actually the same line. |
 |
 |
 |
| In this case, there is exactly one
solution, corresponding to the point of intersection. |
In this case, there are no solutions,
since the graphs do not meet. |
In this case, there are infinitely many
solutions, since every point on one of the lines lies on
both lines. |
The following exercises provide practice in solving each of
the three types of systems.
Exercises
Determine whether each system has one solution, no solution,
or infinitely many solutions by graphing. If the system has one
solution, name it.
| y = 2x + 4 |
y = -x - 3 |
x + 4y = -8 |
| y = 2x + 1 |
y = x + 3 |
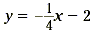 |
| no solution |
(-3, 0) |
infinitely many solutions |
|