Solving Nonlinear Equations by Factoring
In the next example, we will first factor out a common factor.
Example
Solve for w: -w4 + 48w2 = -2w3
| Solution
Step 1 Write the equation in standard form.
Add 2w3 to both sides.
Multiply both sides by -1 to make
the first term positive.
Step 2 Factor.
Factor out the GCF, w2.
Factor the trinomial.
Step 3 Use the Zero Product Property. |
-w4 + 48w2
-w4
+ 2w3 + 48w2
w4 - 2w3 - 48w2 w2[w2 - 2w
- 48] w2[(w - 8)(w + 6)] |
= -2w3
= 0
= 0 = 0 = 0 |
| Set each factor equal to 0.
Step 4 Solve for the variable. |
w2 = 0 or w - 8 = 0 or
|
w + 6 = 0 |
|
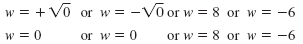 |
So, there are four solutions: 0 (a solution of multiplicity 2), 8, and
-6.
The equation -w4 + 48w2 = -2w3 written in standard form is w4
-2w3 - 48w2 = 0. The graph of the corresponding function,
f(x) = w4 -2w3 - 48w2 is shown.
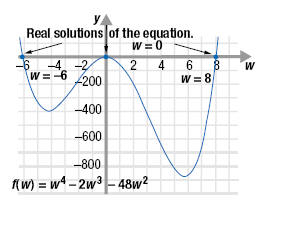
The graph touches or crosses the w-axis at the solutions to the equation:
w= -6, w = 0, and w = 8. |