Computing the Area of Circles
Recall the area of a square is the height times the width. For circles, the “height†and “widthâ€
seem to be continuously varying as you look at the rounded edge. Fortunately there is an easy
way to calculate area of circles: the area of a circle is directly proportional to the size of a
square that encloses it.
Area = pi times radius2
A = π r2
A = 3.14 × r2
How Did They Do It?
The area of a circle, we know, is A = π r2
How did people calculate the area of a circle almost five millennia before integral calculus was
invented?
They probably did it by a method of rearrangement. If you can rearrange a circle into an
equivalent rectangle, then the area is simply given by base times height.
Let us try to use the general idea of rearrangement (as in the figure below) to convert a circle to
a rectangle of equal area. We do this only to help our imagination, not to perform an actual
measurement.
We first cut up a circle into four quarters as shown below, and arrange them as shown. Then
we fill in the spaces between the segments by four matching wedges. The outline of the resulting
weird figure is vaguely reminiscent of a parallelogram. The length of the figure, measured along
the circular arcs, is equal to the circumference of the original circle, 2πr. All we can say with
certainty is the area of this figure is exactly double the area of the original circle.
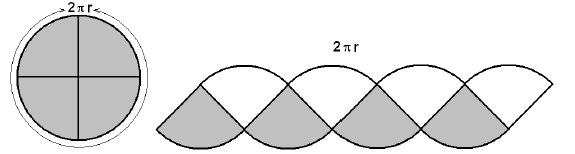
If we now divide the circle not into four, but into very many segments, our weird parallelogram
will resemble a rectangle a little more closely; and the area of the circle is still exactly one half of
the weird parallelogram.
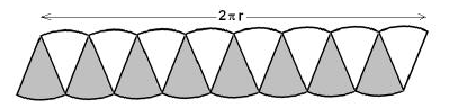
If we continue this process of cutting up the original circle into many more segments, the sides of
the parallelogram will become a straight line. Eventually it will be exactly a rectangle with length
2pr and height r. Therefore the area of the original circle is half of this rectangle, or 2πr2.
|