Solving Systems of Equations - Elimination Using
Multiplication
After studying this lesson, you will be able to:
- Solve systems of equations by elimination using
multiplication.
To Solve a System of Equations By Elimination Using
Multiplication
Sometimes when we try to add equations together, no variables
will cancel out. What we can do is to multiply one or both of the
equations by some number so that a variable will cancel out when
we add the equations together. Then we can follow the regular
steps of addition (elimination):
1. Add the equations together to eliminate one variable.
(Write the equations one over the other and add them together...add
straight down.)
2. Solve for the remaining variable.
3. Substitute the solution into one of the original equations
and solve for the other variable.
Example 1
Solve 3x + 6y = -6, 5x - 2y = 14
Line up the equations and add straight down to eliminate a
variable:
3x + 6y = -6
5x - 2y = 14
No variable cancels, so we need to use multiplication to force
a variable to cancel. If we multiply the second equation by 3,
then the y-variables will cancel:
| 3x + 6y = -6 5x - 2y =
14
|
multiply by 3 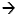
|
3x + 6y = -6 15x
- 6y = 42
18x = 36
x = 2
|
|
Now we can add straight down |
Now we substitute x = 2 into the first equation and solve.
3 (2) + 6y = -6
6 + 6y = -6
6y = -12
y = -2
The solution is (2, -2)
Example 2
Solve 3x + 4y = -25, 2x - 3y = 6
Line up the equations and add straight down to eliminate a
variable:
3x + 4y = -25
2x - 3y = 6
No variable cancels, so we need to use multiplication to force
a variable to cancel. If we multiply the first equation by 3 and
second equation by 4, then the y-variables will cancel:
| 3x + 4y = -25 2x - 3y =
6
|
multiply by 3 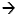 multiply by 4 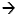
|
9x + 12y = -75 8x
- 12y = 24
17x = -51
x = -3
|
|
add straight down
|
Now we substitute x = -3 into the first equation and solve.
3 (-3) + 4y = -25
-9 + 4y = -25
4y = -16
y = -4
The solution is (-3, -4)
Example 3
Solve 7x -5y = 76, 4x + y = 55
Line up the equations and add straight down to eliminate a
variable:
7x - 5y = 76
4x + y = 55
No variable cancels, so we need to use multiplication to force
a variable to cancel. If we multiply the second equation by 5,
then the y-variables will cancel:
| 7x - 5y = 76 4x + y =
55
|
multiply by 5 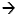
|
7x - 5y = 76 20x
+ 5y = 275
27x = 351
x = 13
|
|
add straight down
|
Now we substitute x = 13 into the first equation and solve.
7(13) - 5y = 76
91 - 5y = 76
-5y = -15
y = 3
The solution is (13, 3) |