Simplifying Rational Expressions

1. need to identify any restrictions on the value of the
variables
a. IE what will make the denominator zero
i. 2xy = 0 .: x = 0, y = 0. .: x,y cannot equal zero are the
restrictions
2. Now reduce the expression into simplest terms.
a. Look at factoring the numerator or the denominator first,
then use exponent laws or cancelling like terms.
i. The value of x can be reduced
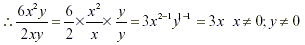
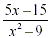 Factoring the numerator
and/or denominator Factoring the numerator
and/or denominator
1. Restrictions , x cannot equal +/- 3.
a. Via inspection or factoring (x-3)(x+3)
2. the expression reduces to 5(x -3)/(x-3)(x+3), which
simplifies to 5/(x+3)
3. Note 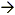 when graphing the function there is no change to the
output of the function. The graph is the same using the
un-simplified form or the reduced form. The reduced form is
easier to work with while doing the graphing by hand when graphing the function there is no change to the
output of the function. The graph is the same using the
un-simplified form or the reduced form. The reduced form is
easier to work with while doing the graphing by hand
Complex Factoring of a rational expression
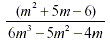
1. Restrictions on the denominator m cannot equal 0, -1/2,
4/3.
a. Factor the denominator 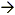 m(6m 2 -5m-4) m(6m 2 -5m-4) 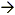 m(m+.5)(m-1.33) m(m+.5)(m-1.33)
2. Nothing can be factored further as there is nothing in
common on top and bottom
1. Factor the numerator and denominator (if possible)
a. Simply
b. Complex
c. Multiple factoring
2. State restrictions of the denominator a. the restrictions
are any value that will make the denominator equal zero
3. Cancel any terms which are multiplied on top and bottom.
4. Write out the final terms and state any restrictions. |