Solving Linear Equations
The techniques shown here should not be attempted until you have become
proficient at solving equations by writing out every step. The more efficient
techniques shown here are not a requirement of algebra, but they can be a labor-saving
tool that will be useful when we solve more complicated problems.
Example
Efficient solutions
Solve each equation.
a) 3x + 4 = 0
b) 2 - (x + 5) = -2(3x - 1) + 6x
Solution
a) Combine steps to solve the equation efficiently.
| 3x + 4 |
= 0 |
|
| 3x |
= -4 |
Subtract 4 from each side. |
| x |
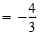 |
Divide each side by 3. |
Check
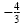 in the original equation:
in the original equation:
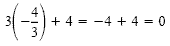
The solution set is
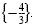
| 2 - (x + 5) |
= -2(3x - 1) + 6x |
|
| -x - 3 |
= 2 |
Simplify each side. |
| -x |
= 5 |
Add 3 to each side. |
| x |
= -5 |
Additive inverse property. |
Check that -5 satisfies the original equation. The solution set is {-5}.
|