Axis of Symmetry and Vertices
Graphs of y = a ( x + d ) 2 + k
Remember that
• when a positive number k is added to a quadratic
function, y = f ( x ) + k , then the parabola shifts up k units,
and
• when k is subtracted from a quadratic function, y = f (
x ) - k , then the parabola shifts down k units.
This is because if the graph of y = f ( x ) has a minimum
point (the parabola opens up), then the minimum value of y = f (
x) + k is k more than the minimum value of y = f ( x ). Moreover,
the minimum values of y = f ( x ) + k and y = f ( x ) occur at
the same x value. So, if the graph of y = f ( x ) has a minimum
point at ( x , y ), then the graph of y = f ( x ) + k has a
minimum point at ( x , y + k ). Since the x value of the minimum
point is unchanged, the equation of the axis of symmetry is also
unchanged.
In the same way, if the quadratic function y = f ( x ) has a
maximum point at ( x , y ) (the parabola opens down), then the
maximum point of the graph of y = f ( x ) + k is ( x , y + k ).
We can now apply this discussion to the functions of the form f (
x ) = a( x + d ) 2 that we have just been studying.
The graphs of quadratic functions of the form y = f ( x ) + k or
y = a ( x + d ) 2 + k have the following properties,
where a is nonzero, and d and k are any numbers.
1. The axis of symmetry is the line x = -d .
2. The vertex is at ( - d , k ). If a is positive, the
parabola opens up and the vertex is a minimum point. If a is
negative, the parabola opens down and the vertex is a maximum
point.
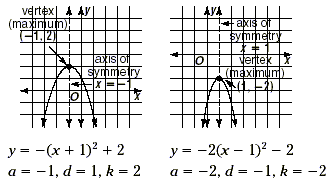
Now notice that if we write y = a( x + d ) 2 + k in
standard form y = ax 2 + bx + c , we can see how to
get the formula 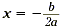 for the axis of
symmetry. for the axis of
symmetry.
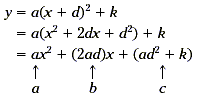
Write this calculation on the chalkboard. Comparing the
coefficient of x , we have
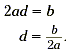
Since the graph of y = a( x + d ) 2 + k has an axis
of symmetry x = -d , this is equal to the equation 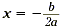 . End this lesson by
providing the following summary. Explain that any quadratic
function y = ax2 + bx + c can be written in the form y
= a( x + d )2 + k by a process called completing
the square. Therefore, these justifications for the
formulas for the axis of symmetry and the vertex work for any
quadratic function. . End this lesson by
providing the following summary. Explain that any quadratic
function y = ax2 + bx + c can be written in the form y
= a( x + d )2 + k by a process called completing
the square. Therefore, these justifications for the
formulas for the axis of symmetry and the vertex work for any
quadratic function.
| Function |
Effect on Graph |
Axis of Symmetry |
Vertex |
| y = ax 2
|
Graph widens ( a < 1) or narrows ( a
> 1). |
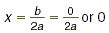 |
y = a (0)
2 = 0 Vertex is at (0, 0).
|
| Graphs opens up ( a > 0) or down ( a
< 0) |
| y = x 2 + c |
Graph moves up. |
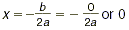 |
y = (0) 2 + c =
c Vertex is at (0, c ).
|
| y = x 2 - c |
Graph moves down. |
y = (0) 2 - c =
-c Vertex is at (0, - c ).
|
| y = ( x + d ) 2
|
Graph moves left. |
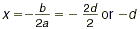 |
y = ( - d + d ) 2
+ 0 Vertex is at ( - d , 0).
|
| y = ( x - d ) 2
|
Graph moves right. |
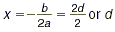 |
y = ( d - d ) 2
+ 0 Vertex is at ( d , 0).
|
| y = a( x + d ) 2
+ k |
Width and direction of graph depend on a. |
x = -d |
y = a ( - d + d ) 2
+ k = 0 + k or k
Vertex is at (-d , k ).
|
| y = a( x - d ) 2
+ k |
Width and direction of graph depend on a. |
x = d |
y = a [ d + ( - d )]
2 + k = 0 + k or k
Vertex is at ( d , k ).
|
|