Point-slope Form for the Equation of a Line
We can find the equation of a line if we know the slope of the line, m, and
a point on the line, (x1, y1). Here’s how we can derive a formula for this.
| Start with the formula for the slope of a line that
passes through the points, (x1, y1), and (x2, y2). |
m |
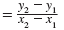 |
| Replace (x2, y2) with (x, y). |
m |
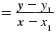 |
| Multiply both sides by x - x1. |
m(x - x1) |
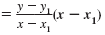 |
| Simplify the right side. |
m(x - x1) |
= y - y1 |
| By tradition, the y terms are written on the left. |
y - y1 |
= m(x - x1) |
The result is called the point-slope form for the equation of a line.
Note:
(x1, y1) represents a point on the line that
we know.
(x, y) represents an unknown point on the
line.
Definition
Point-slope Form for the Equation of a Line
The point-slope form for the equation of a line that passes through
the point (x1, y1) and has slope m is.
y - y1 = m(x - x1)
Note that m, x1, and y1 are constants, and x and y are variables.
The following linear equations are written in point-slope form:
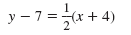 |
Here, (x1, y1) = (-4, 7) and
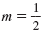 |
| y - 2 = -3(x - 1) |
Here, (x1, y1) = (1, -2) and m = -3. |
|