Factoring quadratics
Introduction
On this leaflet we explain the procedure for factoring
quadratic expressions such as x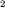 +5 x +6.
+5 x +6.
1. Factoring quadratics
You will find that you are expected to be able to factorize
expressions such as x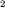 + 5 x + 6.
+ 5 x + 6.
First of all note that by removing the brackets from
( x + 2)( x + 3)
we find ( x + 2)( x + 3) = x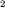 + 2 x + 3 x + 6 = x
+ 2 x + 3 x + 6 = x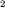 + 5 x + 6 + 5 x + 6
When we factorize x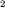 + 5 x + 6 we are looking for the answer ( x + 2)( x + 3).
+ 5 x + 6 we are looking for the answer ( x + 2)( x + 3).
It is often convenient to do this by a process of educated
guesswork and trial and error.
Example
Factorize x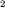 + 6 x + 5. + 6 x + 5.
Solution
We would like to write x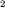 + 6 x + 5 in the form
+ 6 x + 5 in the form
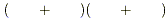
First note that we can achieve the x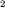 term by placing an x in each bracket:
term by placing an x in each bracket:
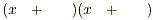
The next place to look is the constant term in x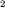 +6
x +5, that is, 5. By removing the brackets you will see that this
is calculated by multiplying the two numbers in the brackets
together. We seek two numbers which multiply together to give 5.
Clearly 5 and 1 have this property, although there are others. So +6
x +5, that is, 5. By removing the brackets you will see that this
is calculated by multiplying the two numbers in the brackets
together. We seek two numbers which multiply together to give 5.
Clearly 5 and 1 have this property, although there are others. So
x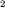 + 6 x +5 = ( x + 5)( x + 1) + 6 x +5 = ( x + 5)( x + 1)
At this stage you should always remove the brackets again to
check.
The factors of x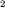 + 6 x + 5 are ( x + 5) and ( x + 1). + 6 x + 5 are ( x + 5) and ( x + 1).
Example
Factorize x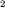 - 6 x + 5. - 6 x + 5.
Solution
Again we try to write the expression in the form
x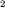 -6 x + 5 = -6 x + 5 = 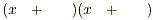
And again we seek two numbers which multiply to give 5.
However this time 5 and 1 will not do, because using these we
would obtain a middle term of +6 x as we saw in the last example.
Trying 5 and 1 will do the trick.
x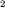 - 6 x +5 = ( x - 5)( x - 1) - 6 x +5 = ( x - 5)( x - 1)
You see that some thought and perhaps a little experimentation
is required.
You will need even more thought and care if the coefficient of
x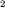 , that is the number in front of the x , that is the number in front of the x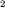 ,
is anything other than 1. Consider the following example. ,
is anything other than 1. Consider the following example.
Example
Factorize 2 x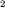 + 11 x + 12. + 11 x + 12.
Solution
Always start by trying to obtain the correct x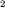 term:
term:
We write
2 x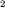 + 11 x +12 = + 11 x +12 = 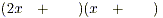
Then study the constant term12. It has a number of pairs of
factors, for example 3 and 4, 6 and 2 and so on. By trial and
error you will find that the correct factorization is
2 x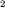 + 11 x + 12 = (2 x + 3)( x + 4) + 11 x + 12 = (2 x + 3)( x + 4)
but you will only realize this by removing the brackets again.
|