Solving Systems of Equations Using Substitution
Examples
Example 1:
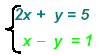
Solve the second equation for x and use the expression as a
replacement for x in the first equation, which gives us an equation in y
alone.
→ x = y + 1 Replace for x in the equation
[1]: 2(y + 1) + y = 5
Solve this equation for y:
| 2y + 2 + y = 5 |
Distributive property |
| 3y + = 3 |
Add Opps |
| y = 1 |
Multiply Recip |
Replace y = 1 in equation [2]: x = ( 1 ) + 1 and find x = 2
Always check in the other equation: 2(2) + (1) = 5

The solution is the point (2, 1) or S = { ( 2, 1) } y = -x + 8 3x − 2y = -1
2x + y = 5 x − y = 1
Example 2:
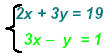
Solve the second equation for y : y = 3x − 1 use the expression on
the right side as a replacement for y in the first equation, which
gives us an equation in x alone.
Substitute the expression for y in the second equation: 2x + 3(3x − 1)
= 19
Solve this equation for x:
| 2x + 9x − 3 = 19 |
Distributive property |
| 11x = 22 |
Add Opps |
| x = 2 |
Multiply Recip |
Replace in equation [2]: y = 3 (2 ) − 1 or y = 5
Always check by replacing both in first equation: 2(2) + 3 (5) = 19

Thus, the solution is the point (2, 5): or S = { ( 2, 5) }
Example 3:
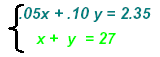
Treat decimal fractions like common fractions. Multiply by LCM.
Multiply equation [1] by LCM =100:
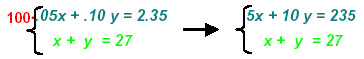
Solve the second equation for x and use the expression x = 27 −
y
as a replacement for x in the new first equation: 5(27 − y) + 10y =
235
Solve this equation for y:
| 135 − 5y + 10y = 235 |
Distributive property |
| 5y = 100 |
Add Opps |
| y = 20 |
Multiply Recip |
Replace y = 20 in equation [2]: x = 27 − ( 20 ) and find x = 7
Always check in the other equation: .05(7) + .10(20) = 2.35

The solution is the point (7, 20) or S = { ( 7, 20) } |