Solving Linear Equations
To solve an equation means to find its solution set. It is easy to
determine whether a given number is in the solution set of an equation, but we
want to have a method for solving equations. The most basic method for solving
equations involves the properties of equality.
Properties of Equality
Addition Property of Equality
Adding the same number to both sides of an equation does not change the
solution set to an equation. In symbols, if a = b then a + c = b + c
Multiplication Property of Equality
Multiplying both sides of an equation by the same nonzero number does not
change the solution set to the equation. In symbols, if a = b and c ≠ 0, then ca
= cb.
Because subtraction is defined in terms of addition, the addition property of
equality also allows us to subtract the same number from both sides. For example,
subtracting 3 from both sides is equivalent to adding -3 to both sides. Because
division is defined in terms of multiplication, the multiplication property of
equality also allows us to divide both sides by the same nonzero number. For
example, dividing both sides by 2 is equivalent to multiplying both sides by
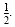
Equations that have the same solution set are called equivalent equations.
In the next example we use the properties of equality to solve an equation by
writing an equivalent with x isolated on one side of the equation.
Example 1
Using the properties of equality
Solve the equation 6 - 3x = 8 - 2x.
Solution
We want to obtain an equivalent equation with only a single x on the left-hand
side and a number on the other side.
| 6 -3x |
= 8 -2x |
|
| 6 -3x - 6 |
= 8 -2x - 6 |
Subtract 6 from each side. |
| -3x |
= 2 - 2x |
Simplify. |
| -3x + 2x |
= 2 - 2x + 2x |
Add 2x to each side. |
| -x |
= 2 |
Combine like terms |
| -1 · (-x) |
= -1 · 2 |
Multiply each side by -1. |
| x |
= -2 |
|
Replacing x by -2 in the original equation gives us
6 -3(-2) = 8 - 2(-2),
which is correct. So the solution set to the original equation is {-2}.
The addition property of equality allows us to add 2x to each side of the
equation in Example 1 because 2x represents a real number.
Caution
If you add an expression to each side that does not always represent a real
number, then the equations might not be equivalent. For example
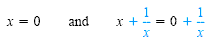
are not equivalent because 0 satisfies the first equation but not the second
one. (The expression
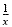 is not defined if x is 0. )
is not defined if x is 0. ) |