Scientific Notation
Objective Learn how to write very large and
small numbers in scientific notation and to compare and order
numbers written in scientific notation.
Scientific notation is a useful topic for many applications.
It also provides a great opportunity to reinforce your
understanding of place value in terms of powers of ten.
Very Large and Very Small Numbers
Let's see some very large and very small numbers. A few
examples are listed.
• The mass of the planet Pluto is roughly
12,900,000,000,000,000,000,000 kilograms.
• The number of molecules in a cubic centimeter of oxygen
at standard temperature and pressure is about
602,000,000,000,000,000,000,000.
• A typical cell membrane is about 0.00000001 meter
thick.
• A large virus has a diameter of roughly 0.0000001
meter.
Each of the numbers shown above contains many zeros. Thus, it
may be difficult to read and compare them. However, there is a
notation that can be used to express all of the zeros in a
simple, easy to read form. Consider the following examples.
Example 1
| 7,000,000,000 (seven
billion) |
= 7 × (one billion) |
| |
= 7 × 10 9 One billion is
equal to 10 9. |
Notice how few symbols are required to write 7 × 10 9
compared to 7,000,000.
Example 2
| 13,000,000 (thirteen
million) |
= 13 × (one million) |
| |
= 13 × 10 6 One billion is
equal to 10 6. |
| |
= 1.3 10 7 1.3 is one tenth of 13. |
Example 3
0.0000056 (fifty-six ten-millionths)
| = 5 × (one millionth) + 6 × (one
ten-millionth) |
|
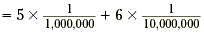 |
|
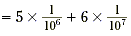 |
1,000,000 = 10 6 and
10,000,000 = 10 7 |
| = 5 × 10 -6 + 6 ×10 -7
|
Laws of Negative Exponents |
| = (5 + 6 ×10 -1 ) × 10
-6 |
Factor 10 -6 . |
| = 5.6 × 10 -6 |
|
Key Idea
Every nonzero number can be written as a number greater than
or equal to one and less than ten times a power of ten.
Definition of Scientific Notation
A number that is written as a number between 1 and 10 times a
power of ten is said to be written in scientific notation.
All of the following numbers are written in scientific
notation.
1.2 ×10 6
2.4 ×10 -5
5.8 ×10 18
The following numbers are not written in scientific notation
because the number in front of the multiplication sign is not
between 1 and 10.
12.5 ×10 12
0.15 ×10 11
235 ×10 -13
|