Linear Equations
Postivite and Negative Slope
Example 1 - Positive slope
y = ½ x + 1
|
x |
y |
|
0 |
1 |
|
1 |
1½ |
|
2 |
2 |
|
3 |
2½ |
|
4 |
3 |
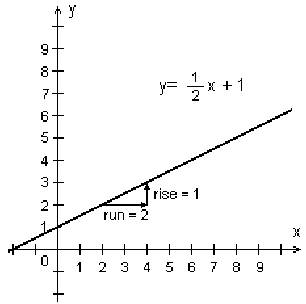
Example 2 - Negative slope
y = -½ x + 1
|
x |
y |
|
0 |
1 |
|
1 |
1½ |
|
2 |
0 |
|
3 |
-½ |
|
4 |
-1 |
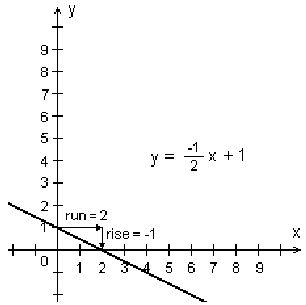
Notice the y- intercept is the same, i.e. 1, for our first
two examples. The only difference between the two
equations is the slope, and not the ‘+1’ on the end.
Note the slope of the line is the same anywhere you look; you can measure the rise and
the run anywhere on the graph. Anywhere you look, when you look at rise ÷ run, you get
the same slope.
Can you think of examples of a negative slope?
|