Dividing Monomials Using the Quotient Rule
You problably know the definition of division to divide signed numbers.
Because the definition of division applies to any division, we restate it here.
Division of Real Numbers
If a, b and c are any numbers with b ≠ 0, then
a ÷ b = c provided that c · b = a.
If a ÷ b = c, we call a the dividend, b
the divisor, and c (or a ÷ b) the quotient.
You can find the quotient of two monomials by
writing the quotient as a fraction and then reducing the fraction. For example,
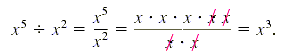
You can be sure that x3 is correct by
checking that x3 · x2 = x5. You can also divide
x2 by x5, but the result is not a monomial:
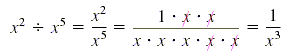
Note that the exponent 3 can be obtained in
either case by subtracting 5 and 2. These examples illustrate the quotient rule
for exponents.
Quotient Rule
Suppose a ≠ 0, and m and n are positive integers.
If m ≥ n, then
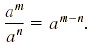
If n > m, then
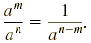
Note that if you use the quotient rule to
subtract the exponents in x4 ÷ x4, you get the exporession
x4 - 4, or x0, which has not been defined yet. Because we
must have x4 ÷ x4 = 1 if x ≠ 0, we define the zero power
of a nonzero real number to be 1. We do not define the expression 00.
Zero Exponent
For any nonzero real number a, a0 =
1.
Example 1
Using the definition of zero exponent
Simplify each expression. Assume that all variables are nonzero real numbers.
a) 50
b) (3xy)0
c) a0 + b0
Solution
a) 50 = 1
b) (3xy)0 = 1
c) a0 + b0 = 1 + 1 = 2
With the definition of zero exponent the quotient rule is valid for all
positive integers as stated.
Example 2
Using the quotient rule in dividing monomials
Find each quotient.

Solution
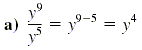
Use the definition of division to check that y4 · y5 =
y9.
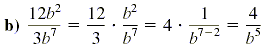
Use the definition of division to check that
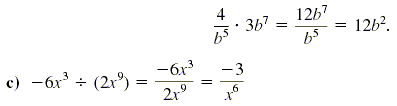
Use the definition of division to check that
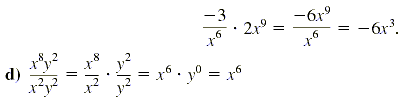
Use the definition of division to check that x6 · x2y2
= x8y2.
|