Simplifying Fractions
Examples with solutions
Example 1:
Simplify 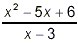 . .
solution:
There is no possibility of factoring the denominator further
here, since neither term in the denominator is a product. The
numerator is a trinomial, and so possibly can be factored into a
product of two binomials:
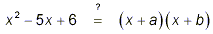
As explained earlier in these notes, for this to be possible,
we would need to find numbers ‘a’ and ‘b’
such that a + b = -5 and ab = 6. You have probably already
noticed that a = -2 and b = -3 will work. It is easy to confirm
that
(x – 3)(x – 2) = x 2 – 5x + 6.
So, our original fraction becomes
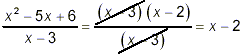
in simplest form.
Example 2:
Simplify 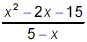 . .
solution:
Proceeding as in the previous example, we quickly find that
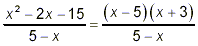
At first, it may not appear that any cancellation is possible
because neither of the factors in the numerator look the same as
the denominator. However, recall that (x – 5) = -(5 –
x). So, we can write our fraction here as
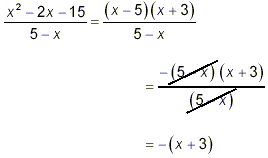
since now the presence of the common factor (5 – x) in
the numerator and denominator is obvious. Cancelling that common
factor leads to the final result.
Example 3:
Simplify 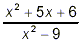 . .
solution:
By now, you are very familiar with the process: factor the
numerator and denominator and cancel common factors. Here this
gives
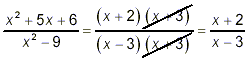
as the final answer.
Example 4:
Simplify 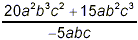 . .
solution:
Factoring and taking into account for the minus sign in the
denominator gives
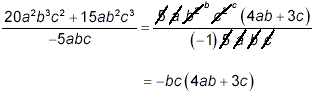
as the final simplified result. |