Evaluation of Simple Formulas
To evaluate an algebraic expression means to
substitute given numbers for each literal symbol in the
expression and then carry out the indicated arithmetic to obtain
a single numerical value for the entire expression.
Example:
Evaluate 3x 2 – 5x + 7 for x = 2 and for x =
-5.
solution:
When x = 2, the expression becomes
3x 2 – 5x + 7 = 3(2) 2 – 5(2)
+ 7
= 3(4) – 5(2) + 7
= 12 – 10 + 7
= 9
When x = -5, we get
3x 2 – 5x + 7 = 3(-5) 2 –
5(-5) + 7
= 3(25) – 5(-5) + 7
= 75 + 25 + 7
= 107
Notice the use of brackets where convenient, particularly to
ensure the correct handling of negative numbers.
Example:
Evaluate 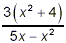 when x = -3. when x = -3.
solution:
Substituting
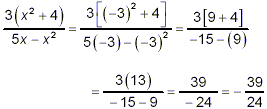
We needed to take considerable care here to handle the
negative numbers correctly.
Example:
Evaluate 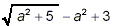 when a = 2 and when a
= -2. when a = 2 and when a
= -2.
solution:
When a = 2, we get
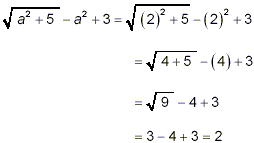
When a = -2, we get
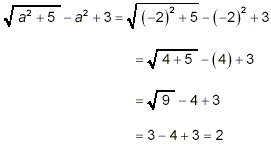
So, we get the same value for both a = +2 and for a = -2.
Although (3) 2 = 9 and (-3) 2 = 9, so that
both +3 and -3 are square roots of 9, the symbol 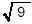 stands for the positive
square root of 9 by definition. Thus, stands for the positive
square root of 9 by definition. Thus, 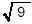 is always considered to
be +3. is always considered to
be +3.
Example:
Evaluate x 2 – 5x + 4 for x = 0, 1, 2, 3, 4,
and 5.
solution:
Here it is probably easiest to just make a table summarizing
our results:
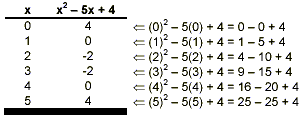
|