Solving Quadratic Equations Using the Square Root
Property
Example
Solve using the Square Root Property: 16x2 - 24x + 9 = 81
Solution
| Step 1 Write the equation in the form x2
= a.
The first and last terms of the
trinomial are perfect squares. |
(4x)2 - 24x + (3)2
(4x)2 - 2(4x)(3)x + (3)2 |
= 81 = 81 |
| Since the trinomial has the form
a2 - 2ab + b2, it is a perfect square
trinomial. |
|
|
| A perfect square trinomial can
be written as the product of two
identical binomials. |
(4x - 3)(4x - 3)
(4x - 3)2 |
= 81 = 81 |
| Step 2 Use the Square Root
Property. Step 3 Write each answer in simplified form. |
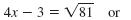 |
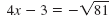 |
| Simplify 81.
To solve for x, add 3 to both sides.
Divide both sides by 4. |
4x - 3 = 9 or
4x = 12 or
x = 3 or |
4x - 3 = -9 4x = -6
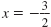 |
| Step 4 Check each answer.
We leave the check to you. |
|
|
So, the two solutions of 16x2 - 24x + 9 = 81 are 3 and
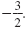
Note:
This equation can also be solved by
factoring. We first write the equation in the
form ax2 + bx + c = 0.
16x2 - 24x + 9 = 81
16x2 - 24x - 72 = 0
8(2x2 - 3x - 9) = 0
8(2x + 3)(x - 3) = 0
2x + 3 = 0 or x - 3 = 0
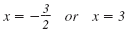 |