Adding and Subtracting Fractions
Addition and subtraction of algebraic fractions works
basically the same way as does addition and subtraction of simple
numerical fractions:
(i.) rewrite all of the fractions as mathematically equivalent
fractions, but having the same denominator (ideally, the simplest
such common denominator).
(ii.) combine the numerators of these fractions as indicated
(adding and subtracting), retaining the common denominator.
When we work with algebraic fractions, there is then often a
third very important step:
(iii.) simplify the resulting fraction as much as possible. It
is always necessary to make sure that once the
addition/subtraction step is completed, you make a reasonable
effort to simplify the result. Usually this simplification step
will be made very much easier if you take care in step (i.) to
make sure that you have used the simplest possible common
denominator. We will illustrate the process for determining that
simplest possible denominator when the fractions to be
added/subtracted are algebraic fractions. You will see that the
strategy is essentially the same as the strategy used to
determine the least common denominator when adding or subtracting
numerical fractions, except that now symbolic factors may occur
as well as numerical factors.
Example 1: Combine and simplify: 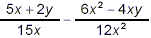
solution:
Here, the two denominators share some factors in common and so
the simplest common denominator for these fractions is not simply
the product of the two denominators. Noting that
15x = (3)(5)(x)
and
12x 2 = (2 2)(3)(x 2)
we conclude that the simplest common denominator here is (2
2)(3)(5)(x 2) = 60x 2. So
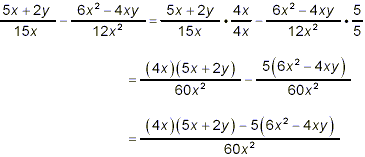
The numerator is a difference of two terms, and so we try
multiplying to remove the brackets followed by collection of like
terms in hope of being able to achieve some simplification.
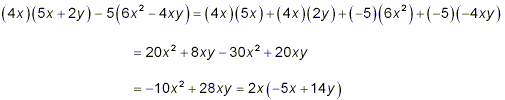
When the like terms were combined, we noticed that the two
terms remaining shared a common factor of 2x, which has been
factored out in the last line. Thus, our original difference of
two fractions becomes
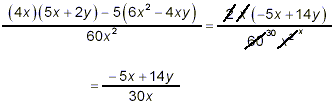
as the final answer. Since what is left in the numerator
cannot be factored further, this is as simple as we can get for
the final answer.
Example 2:
Simplify 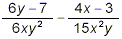
solution:
As mentioned before, the instruction to “simplify”
here means combine the two fractions into a single fraction, and
reduce that resulting single fraction to as simple a form as
possible. We’ve now done several examples of this type, so
here we’ll more or less just show the work without including
a lot of discussion. This would be a good example for you to try
as a practice exercise before you look at our solution given
below.
The two denominators factor as
6xy 2 = (2)(3)(x)(y 2)
and
15x 2 y = (3)(5)(x 2)(y)
Thus, the simplest common denominator is
(2)(3)(5)(x 2)(y 2) = 30x 2 y
2
So, going back to the original problem
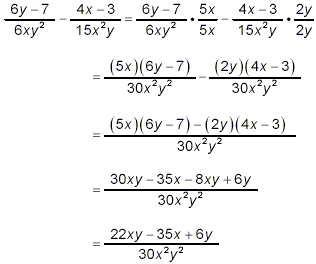
There is no obvious way to factor this numerator, so it does
not appear that any further simplification of this fraction is
possible. So, the last form above must be the requested final
answer.
Example 3:
Simplify 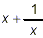
solution:
Some people experience an overwhelming temptation here to
simply cancel the x’s:
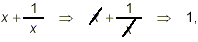
confusing this addition problem with the much simpler
multiplication problem
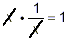
where the cancellation to get the simple result ‘1’
is justified. However, no such quick cancellations can be done in
the addition problem we have here because the two x’s
aren’t even part of the same fraction! In fact, the first
term here is not even a fraction.
Perhaps the clearest way to proceed is to turn the first term
into a fraction with denominator equal to 1, and then apply the
methods of the previous examples for adding two fractions. We get
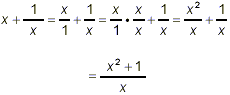
This is the final answer, since the numerator cannot be
factored further and so there is no additional simplification
possible.
Example 4:
Combine and simplify: 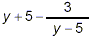
solution:
Again, we start by turning this problem into a problem with
two fractions, and then we just apply the methods already
illustrated in the previous examples.
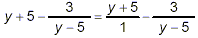
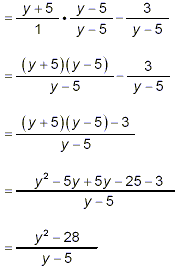
The simple form of this last fraction is obtained from the
previous step by collecting like terms in the numerator. The
terms -5y + 5y add up to zero y’s, and the two numbers sum
to -28. The numerator of the final fraction shown above, y 2
– 28, cannot be factored further to give a form that leads
to cancellations with the denominator, so this must be the
required final answer. |